
Tuning of musical scales is a matter that has (over a long period of development) resulted in a great many systems, among them the western twelve-tone, equal tempered scales. Temperament can only be understood in relation to the pure intervals that are attributed to ancient greek mathematician Pythagoras and his concept of »Harmony of the Spheres«.
Aside from tuning issues the perceived sound of instruments is related to the harmonic content of their sound waves. Wavetable and some additive synthesizers have a very distinct sound and I've come to the conclusion that they owe this to the perfect harmonic series they produce. The fixed phase relation might also have some influence, but this would only be noticeable when the the spectral amplitudes are modulated.
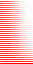
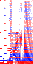
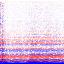
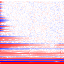
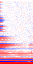
Starting with the fundamental at the bottom and the first wave in the table at the left, each pixel in the images represents the spectral amplitude of a single partial. The color of the pixel encodes the sign (blue is negative and red is positive), while the intensity encodes the magnitude. The magnitude information has been compressed with a function (asinh) that behaves linearly about zero and logarithmic for larger values, because otherwise you wouldn't be able to see much detail. The greyscale images drop the sign information. Depending on screen resolution the images are best viewed at 3x to 4x magnification. Make sure you viewer does not smooth scaled pictures, you should see »blocky« images.
 Synthetic Saw with
sign magnitude information or only
with magnitude information
Synthetic Saw with
sign magnitude information or only
with magnitude information

 with
sign magnitude information or only
with magnitude information
with
sign magnitude information or only
with magnitude information
 with sign magnitude information
or only
with magnitude information
with sign magnitude information
or only
with magnitude information

 with sign
information or only with
magnitude information
with sign
information or only with
magnitude information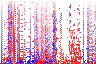 with sign magnitude information or
only with magnitude
information
with sign magnitude information or
only with magnitude
information with sign magnitude information or
only with magnitude
information
with sign magnitude information or
only with magnitude
information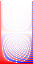 Continously variable saw
wave with sign magnitude
information or only with
magnitude information
Continously variable saw
wave with sign magnitude
information or only with
magnitude information
 with sign magnitude information
or only
with magnitude
information
with sign magnitude information
or only
with magnitude
information

The relation of the various scales and harmonic series can perhaps be more easily understood from this visualization [PDF 9k] [PNG 11k] showing the harmonic relation on a musical scale; it's still a very busy chart. As guidelines the equal tempered scale and the scale resulting from the pythagorean pure intervals are shown. A pure or pythagorean interval is one where the frequency ratio is of two small integers. The pythagorean scale c : d : e : f : g : a : b : c is given by 1/1 : 9/8 : 5/4 : 4/3 : 3/2 : 5/3 : 15/8 : 2/1. The most pure interval aside from the octave is hence the pythagorean fifth, given by a frequency ratio of 3/2. A comparison of progressions of pure intervals reveals that it is (mathematically) impossible to arrive at exactly the same point: A circle of twelve pythagorean fifths is about 74/73 sharp of seven pythagorean octaves, the difference is known as the pythagorean comma. Likewise four pythagorean fifths are 81/80 sharp of a pythagorean third two octaves up, known as the syntonic comma. Looking at the chart you'll find similar »commas« with the other pythagorean intervals, most notably the fourth (I don't know if these »commas« have their own names).
The second part of the chart shows the series of 255 perfect harmonics and a series of 133 »stretched« harmonic, relating to an ideal string (and wavetable synthesis) and a stiff, but massless string. The amount of stretch (or dispersion) in the latter has been arbitrarily set to amount to about 33 cent (a third of a semitone) over four octaves, a number that seems to be agreed upon for upright piano strings. The higher harmonics are almost certainly wrong for a piano, as a piano string has finite mass. Mass leads to a compression of harmonics, but does not dominate over the stretching effect of the stiffness at least in the audio range. I haven't got hold of a spectrum for a piano string that would allow to assess the relative importance of mass and dispersion - please let me know if you have one. The massless approximation seems to be good enough for a Violin string, see the section on »Modeling the stiffness of the string« in the paper Impact of String Stiffness on Virtual Bowed Strings by Stefania Serafin and J. O. Smith.